实验5 - RSA-OAEP 测试样例
1. 根据学号最后一位选择p, q
根据学号末位选择p,q
2. 根据学号输出下一个素数作为RSA私钥d
下一个素数
3. 根据RSA私钥d求出公钥e
求解d关于模phi_n的逆元e即可。
求模逆元
4. 使用PPT给出的简单OAEP填充法对姓名全拼进行填充
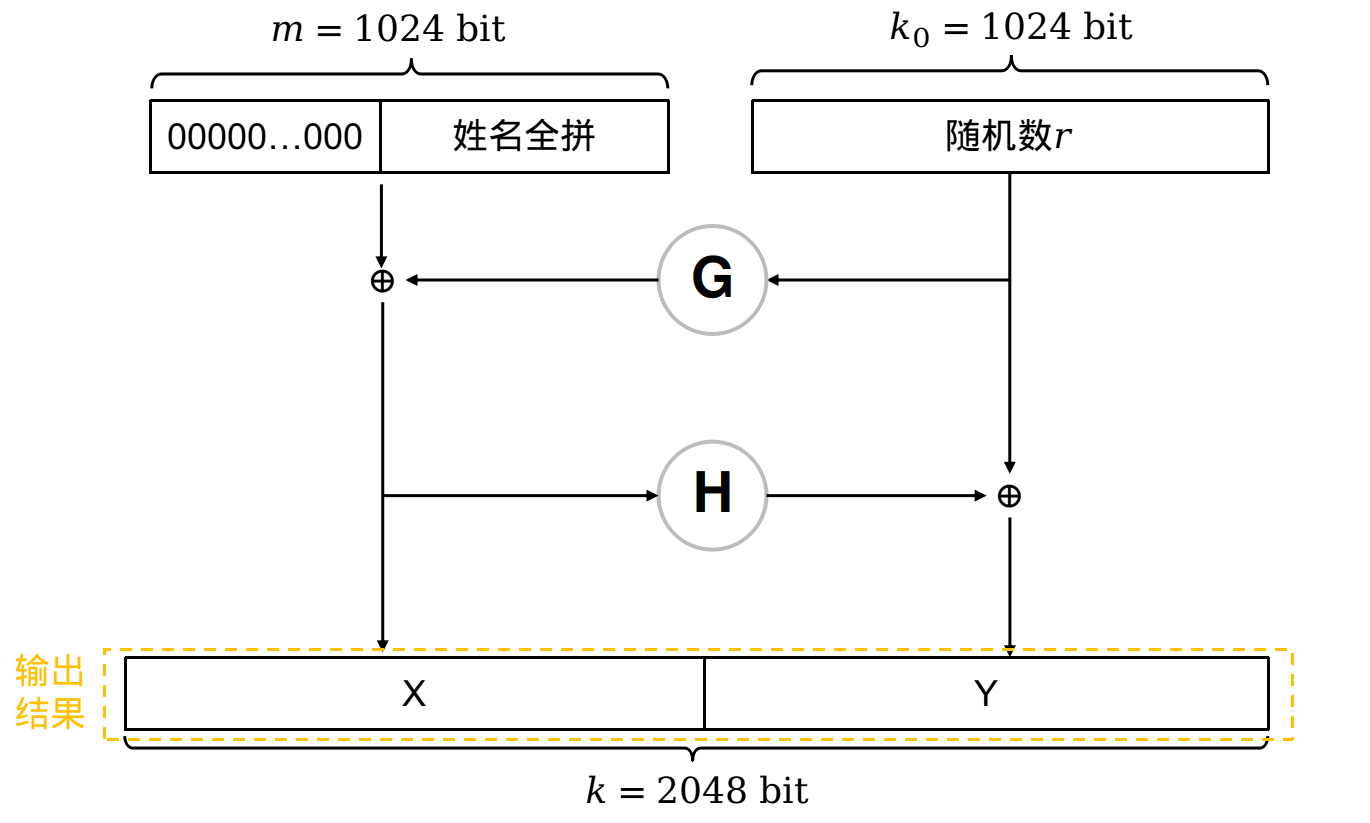
编码过程:先对姓名的全拼编码(ASCII或UTF-8, 因为都是英文字符,所以编码后的结果都是一样的)后的字节序列前面补0直至大小为1024 bit(128字节)。然后选取一个1024bit大小的随机数r和填充后的姓名全拼进行两次的掩码(G和H是掩码生成函数MGF)。过程如下图所示。
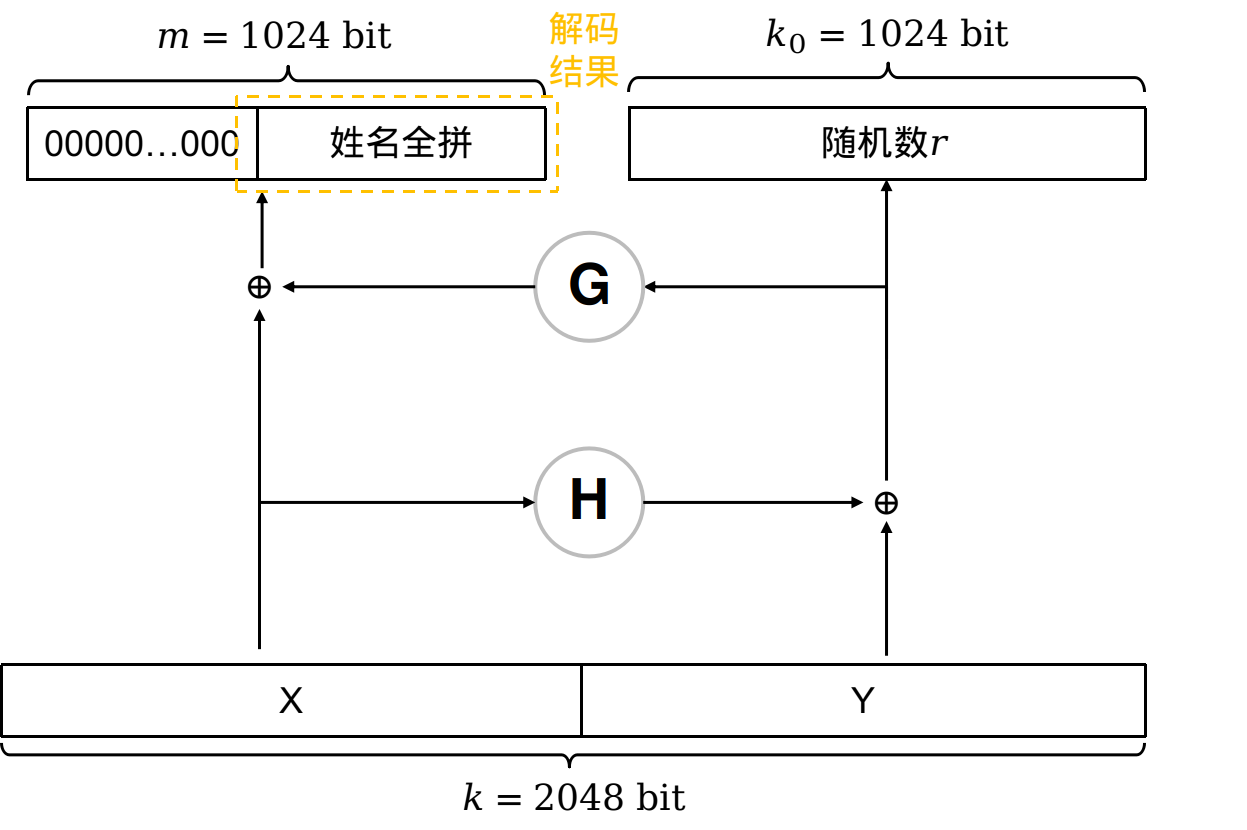
解码过程是编码过程的逆过程。我们对2048bit的待解码数据等分成两个1024bit长的字节序列X和Y,然后进行下图的掩码操作。 最终我们需要的解码结果为下图的黄色方框。
G和H的实现我们使用下图的方式进行,这里直接摘抄了PPT的内容:

其中,H'为哈希函数SHA-256,因此,G和H的输出就是四次SHA-256迭代、拼接,然后再将前两个字节置0并输出。为了便于展示,上图的H'(m||0)中的0其实用到了四个字节,即实际上是H'(m||0x00000000)。同理,H(m||1)其实是H(m||0x00000001),H(m||2)其实是H(m||0x00000002),H(m||3)其实是H(m||0x00000003)。
下面给出了示例程序,可以看到,无论输入和随机数r怎么变化,输出的结果中前两个字节始终为0x00。
简易OAEP编码/解码(PPT的做法)
5. 基于简单OAEP填充的RSA加密/解密
对姓名全拼进行了OAEP填充后,我们就可以开始进行RSA的加密和解密操作了。下面是示例程序,注意输入的待加密数据不用自己事先进行OAEP填充。
基于简易OAEP填充的RSA加密/解密
补充1:RFC8017的EME-OAEP填充法
有兴趣的同学可以进一步实现RFC8017给出的EME-OAEP填充方法,具体实现文档为:https://datatracker.ietf.org/doc/html/rfc8017#section-7.1.1。
文档给出了详细的OAEP填充流程。这里简单解释一下,EME-OAEP有两个输入:消息M和标签label(可为空)。我们将EME-OAEP输出的长度表示为k,OAEP所选用的哈希函数(用于对标签label计算散列值)输出的长度为hLen,消息M的长度为mLen。因此,编码的流程为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
EME-OAEP encoding:
a. If the label L is not provided, let L be the empty string. Let lHash = Hash(L), an octet string of length hLen (see the note below).
b. Generate a padding string PS consisting of k - mLen - 2hLen - 2 zero octets. The length of PS may be zero.
c. Concatenate lHash, PS, a single octet with hexadecimal value 0x01, and the message M to form a data block DB of length k - hLen - 1 octets as
DB = lHash || PS || 0x01 || M.
d. Generate a random octet string seed of length hLen.
e. Let dbMask = MGF(seed, k - hLen - 1).
f. Let maskedDB = DB \xor dbMask.
g. Let seedMask = MGF(maskedDB, hLen).
h. Let maskedSeed = seed \xor seedMask.
i. Concatenate a single octet with hexadecimal value 0x00, maskedSeed, and maskedDB to form an encoded message EM of length k octets as
EM = 0x00 || maskedSeed || maskedDB.
这里给出了RFC8017编码过程的示意图。其中lHash为标签label的Hash值,PS为全0的填充字节,seed为一个随机选取的种子,MGF则为掩码生成函数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
_________________________________________________________________
+----------+------+--+-------+
DB = | lHash | PS |01| M |
+----------+------+--+-------+
|
+----------+ |
| seed | |
+----------+ |
| |
|-------> MGF ---> xor
| |
+--+ V |
|00| xor <----- MGF <-----|
+--+ | |
| | |
V V V
+--+----------+----------------------------+
EM = |00|maskedSeed| maskedDB |
+--+----------+----------------------------+
_________________________________________________________________
解码的流程便是上述过程中的逆过程。这里不再赘述,可参考RFC 8017文档进行实现。
有关MGF的实现我们在PPT上给出了,这里不再赘述。因此,EME-OAEP需要用到两个Hash函数:一个用于对label计算散列值,一个用于MGF的底层散列函数。在本次实验中为了方便,上述两个Hash函数都采用SHA-256。
EME-OAEP编码/解码(RFC8071的做法)
补充2:RFC8017的RSAES-OAEP加密/解密
根据上述的EME-OAEP,我们就可以实现了实用的RSA加密方案——RFC8017的RSAES-OAEP,下面给出了实例程序。